Výzva k pochopeniu výpočtovej neredukovateľnosti: Pohľad z hĺbky
Ponor do výpočtovej neredukovateľnosti s Jonathanom Gorardom odhaľuje komplexné témy, ako formalizácia, rola pozorovateľa a prepojenie s teóriou kategórií. Zjednodušenie systémov je otázne; kľúčom k pochopeniu môže byť vzťah medzi pozorovaným a pozorovateľom.
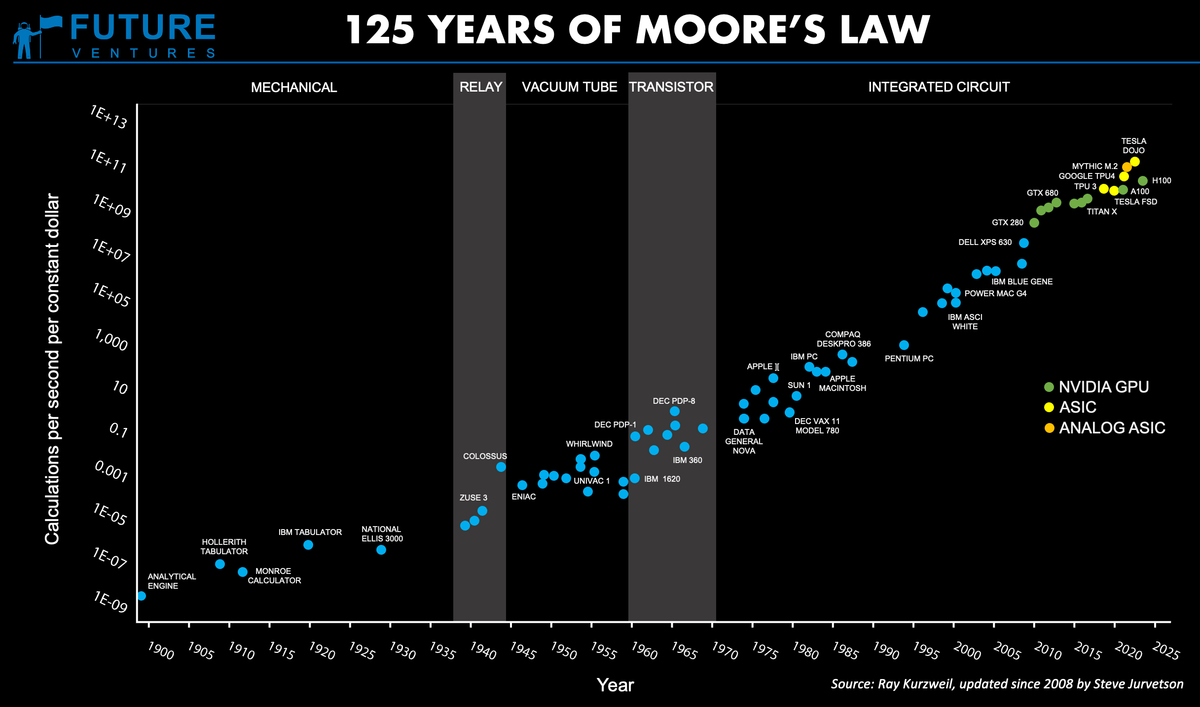
V poslednom videu s Jonathanom Gorardom sa Curt Jaimungal ponoril do fascinujúcej oblasti výpočtovej neredukovateľnosti a jej prepojenia s teóriou kategórií. Diskusia sa dotkla komplexných tém, ako je formalizácia neredukovateľnosti, úloha pozorovateľa v systéme a potenciálne implikácie pre fyziku Stephena Wolfrana. Cieľom bolo odhaliť hlbšie pochopenie toho, čo znamená, keď systém vykazuje neredukovateľné správanie – teda, keď ho nemožno zjednodušiť na menej zložitý algoritmus.
Kľúčové poznatky
- Neredukovateľnosť a teória kategórií: Hoci Stephen Wolfram vidí v teórii kategórií spôsob, ako obísť výpočtovú neredukovateľnosť, Jaimungal nesúhlasí. Tvrdí, že teória kategórií skôr opisuje proces tvorby, než zjednodušenie.
- Formálna definícia: Neredukovateľnosť je formálne definovaná ako otázka, či existuje Turingov stroj s menším počtom krokov na dosiahnutie rovnakého výstupu ako iný.
- Hľadanie neredukovateľnosti v Rule 30 a Rule 110: Rule 30 je stále nepreukázaný ako neredukovateľný, zatiaľ čo Rule 110 je jediným elementárnym celulárnym automatom, ktorý bol preukázaný ako univerzálny (a teda aj neredukovateľný).
- Pozorovateľská závislosť: Významné je definovanie ekvivalencie v rámci systému, pretože drobné zmeny môžu vytvárať falošné príčinné vzťahy. Úroveň sofistikovanosti pozorovateľa ovplyvňuje to, čo považujeme za ekvivalentné.
- Dva extrémy pozorovateľských rolí: Diskusia sa zamerala na dva extrémne pohľady na pozorovateľa: jeden, kde je pozorovateľ banálny a všetky výpočty prebiehajú v systéme, a druhý, kde je systém banálny a všetky výpočty vykonáva sofistikovaný pozorovateľ.
Hlbší ponor do konceptov
Výpočtová neredukovateľnosť je základný kameň komplexity. Ak je algoritmus neredukovateľný, znamená to, že neexistuje žiadny jednoduchší spôsob, ako ho vykonať. To má hlboké dôsledky pre naše chápanie sveta okolo nás, pretože mnoho systémov v prírode – od počasia až po ľudský mozog – sa zdá byť neredukovateľných.
Jaimungalova práca "A Functorial Perspective on Multicomputational Irreducibility" skúma prepojenie medzi teóriou kategórií a výpočtovou neredukovateľnosťou. Teória kategórií je matematický rámec, ktorý študuje vzťahy medzi rôznymi matematickými štruktúrami. Jaimungal navrhuje "tagovanie" morfizmov (prepojení) v teórii kategórií informáciami o výpočtovej zložitosti – napríklad počtom operácií Turingovho stroja. Týmto spôsobom by sme mohli vytvoriť nový druh metrickej štruktúry a definovať neredukovateľnosť na základe aditívnych komplexít.
Dôležitou témou je aj úloha pozorovateľa. Jaimungal argumentuje, že dva extrémne pohľady – banálny systém so sofistikovaným pozorovateľom a banálny pozorovateľ s komplexným systémom – sú v podstate nepozorovateľné. To vedie k zaujímavému filozofickému rozhovoru o vzťahu medzi subjektívnym pozorovaním a objektívnou realitou. Táto myšlienka pripomína historický konflikt medzi empirizmom (ktorý kladie dôraz na objektívne systémy) a racionalizmom (ktorý zdôrazňuje interné reprezentácie).
Zhrnutie a úvahy
Diskusia s Jonathanom Gorardom ponúkla fascinujúci pohľad do oblasti výpočtovej neredukovateľnosti. Jaimungalova práca predstavuje inovatívny prístup k pochopeniu tohto komplexného javu, pričom zdôrazňuje dôležitosť teórie kategórií a úlohy pozorovateľa.
Je zaujímavé zamyslieť sa nad tým, či je možné dosiahnuť skutočné zjednodušenie zložitých systémov alebo či sme navždy odsúdení čeliť neredukovateľnosti. Možno, ako naznačuje Jaimungal, kľúč k pochopeniu leží v lepšom porozumení vzťahu medzi pozorovateľom a pozorovaným.
Pre tých, ktorí sa chcú o túto tému dozvedieť viac, odporúčam navštíviť Substack Curt Jaimungala, kde nájdete hlbšie ponory do súvisiacich tém a zapojenie do komunity.
Zdroje
- Originálne video
- Jonathan Gorard: Quantum Gravity & Wolfram Physics Project - YouTube
- ekonomista.com
- Curt Jaimungal | Substack
- Curt Jaimungal - YouTube
- twitter.com
- 💡 Teórie Všetkého s Curtom Jaimungalom
Hodnotenie článku:
Výzva k pochopeniu výpočtovej neredukovateľnosti: Pohľad z hĺbky
Osoby v článku
Približne 162 gCO₂ bolo uvoľnených do atmosféry a na chladenie sa spotrebovalo 0.81 l vody za účelom vygenerovania tohoto článku.
Komentáre ()