Iné

Terrence Tao o matematike, AI a najťažších problémoch

Terrence Tao o najťažších problémoch v matematike, AI a budúcnosti. Diskusia s Lexom Fridmanom prináša pohľad na parciálne diferenciálne rovnice, teóriu čísel a potenciál AI pri riešení zložitých výziev.

Photo by 14829735@N00/Flickr

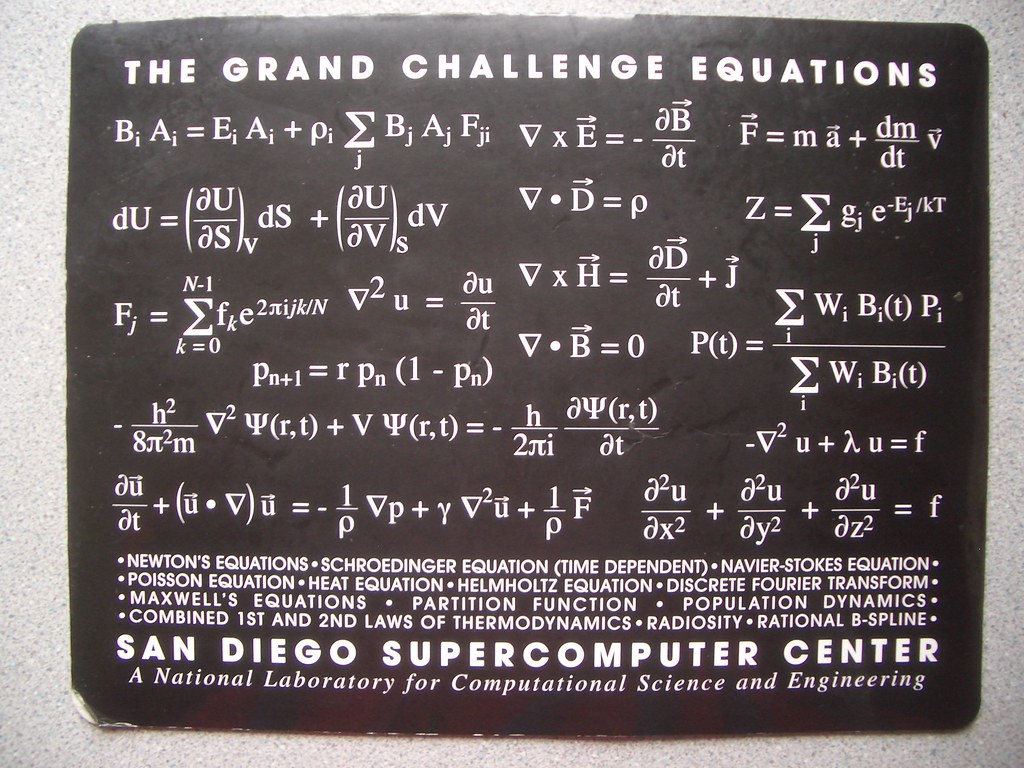
Terence Tao, jeden z najuznávanejších matematikov súčasnosti, sa v rozhovore s Lexom Fridmanom ponoril do fascinujúceho sveta matematických problémov, od riešenia starých hádankám až po spekulácie o budúcnosti AI. Diskusia priniesla kľúčové poznatky o náročných výzvach v oblasti parciálnych diferenciálnych rovníc (PDE), teórie čísel a geometrii, pričom Tao načrtol aj svoje myšlienky na úlohu umelej inteligencie pri riešení týchto problémov. Tento článok sumarizuje kľúčové body rozhovoru a ponúka hlbší pohľad do sveta matematiky a jej prepojení s fyzikou a technológiou.

Kľúčové Poznámky z Rozhovoru

Matematika na Hranici: Tao vysvetľuje, že matematici často pracujú na problémoch "na hranici" medzi riešiteľnosťou a beznádejou – tých, kde existujúce techniky dokážu vyriešiť 90% výzvy.
Problém CA a Hádanky s Ihlou: Tao sa zameral na históriu problému CA (Collatz) a zaujímavé hádanky ako "ihla U-turn", ktoré ilustrujú prepojenie jednoduchých otázok s komplexnými matematickými konceptami.
Navier-Stokes Rovnice a Singularita: Diskusia sa venovala aj notoricky známeho problému Navier-Stokes, ktorý ponúka milióndolárovú odmenu za dokázanie alebo vyvrátenie "blow-up" – náhleho singularitného správania sa prúdov tekutín.
AI a Matematika: Tao načrtol potenciál AI ako asistenta pre matematikov, najmä pri formalizácii dôkazov a hľadaní lemmat, ale zároveň upozornil na súčasné obmedzenia.
Dôležitosť Adaptability a Otvorenosť: Tao zdôraznil potrebu adaptability v kariérnych cestách a otvorenosť novým technológiám a prístupom k riešeniu problémov.

Hlbší Pohľad do Matematických Výziev

Tao začal rozhovor vysvetlením, že matematika sa často zaoberá problémami, ktoré sú "na hranici" toho, čo je možné vyriešiť s existujúcimi nástrojmi. Tento prístup umožňuje matematikom postupne posúvať hranice poznania a objavovať nové techniky.

Problém CA (Collatz) predstavuje fascinujúci príklad takého problému. Ide o jednoduchý algoritmus, ktorý iteratívne aplikuje pravidlá 3n+1 alebo n/2 na ľubovoľné kladné celé číslo. Otázka, či tento proces vždy končí v cykle alebo diverguje do nekonečna, zostáva nevyriešená a predstavuje pre matematikov výzvu.

Hádanka s ihlou U-turn je ďalším zaujímavým príkladom. Táto hádanka sa pýta na minimálnu plochu potrebnú na otočenie ihly (napríklad automobilu) okolo bodu. Počiatočné riešenia naznačovali, že plocha by mala byť π/4 s rotáciou alebo π/8 s trojbodovým zákrutom. Mazikovich však dokázal, že plocha môže byť teoreticky arbitrárne malá, čo vedie k prekvapujúcym prepojeniam s PDE, teóriou čísel a geometriou.

Navier-Stokes rovnice sú základným pilierom dynamiky tekutín a opisujú pohyb tekutín ako plynov a kvapalín. Milióndolárová odmena Clay Mathematics Institute za dokázanie alebo vyvrátenie "finite time blow-up" (náhleho singularitného správania sa) je dôkazom náročnosti tohto problému. Tao navrhol konštrukciu tzv. "liquid computer" – analógie s počítačom postaveným z tekutín, ktorý by mal pomôcť lepšie pochopiť výzvy spojené s dokázaním globálnej regularitu Navier-Stokes rovníc.

AI a Budúcnosť Matematiky

Tao sa vyjadril k rastúcemu vplyvu umelej inteligencie na matematiku. Hoci súčasné AI modely majú obmedzenia, Tao predpovedá, že už o niekoľko desaťročí budú AI aktívne zapojené do matematických spoluprác a potenciálne prispejú k významným prelomom, ktoré by mohli byť hodné Fields Medaily. Poukazuje na nástroje ako Lean, formálny programovací jazyk, ktorý umožňuje overovanie dôkazov a uľahčuje spoluprácu medzi matematikmi.

Zmysel Matematiky a Veda o Poznanie

Tao sa zamyslel aj nad širším kontextom matematiky a jej vzťahu k fyzike a vede o poznanie. Poukázal na to, že matematika je primárne zameraná na vytváranie modelov a skúmanie ich dôsledkov, zatiaľ čo fyzika sa zaoberá zbieraním pozorovaní a navrhovaním modelov, ktoré ich vysvetľujú. Použil Platónovu alegóriu o jaskyni, aby ilustroval, že matematici (a ľudia všeobecne) vnímajú iba odtiene skutočnosti, ale cieľom je posunúť modely bližšie k realite prostredníctvom pozorovaní a opustenia prvotných intuícií.

Odporúčania a Zamyslenia

Rozhovor s Terencem Taom ponúka cenné poznatky pre všetkých, ktorí sa zaujímajú o matematiku, fyziku a budúcnosť AI. Taoho zdôraznenie adaptability, otvorenosť novým prístupom a schopnosť učiť sa z chýb sú dôležité ponaučenia nielen pre mladých matematikov, ale aj pre každého, kto čelí komplexným výzvam v živote.

Zdroje: